[DS/자료구조]세그먼트 트리(Segment Tree)

세그먼트 트리란 통계 트리라고도 하며 배열의 구간 합을 구할 때 적합한 구조입니다!

 

백준 2042번 문제가  세그먼트 트리를 사용하는데 세그먼트 트리를 공부하고 풀어보면 좋을 것 같습니다 :) 저는 나동빈님의 블로그 글을 보고 공부하여 문제를 풀었고 그것을 제 블로그에 기록했습니다. 참고로 아래 설명에 나오는 제 코드는 java로 작성한 코드입니다!

 

 

[예시]

배열 {1, 2, 3, 4, 5, 6, 7, 8}의 구간합을 세그먼트 트리로 나타내면 아래와 같습니다.

 

segment tree

 

루트 노드는 모든 구간의 합으로 이루어져 있고 이는 왼쪽과 오른쪽 노드의 합을 의미합니다.

이것을 이용하여 세그먼트 트리를 생성하는 메소드를 작성해 보겠습니다.

 

 

 

세그먼트 트리 생성(init)

long init(int start, int end, int node) {
    if (start == end) return tree[node] = arr[start];    
    int mid = (start + end) / 2;                       
    return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}

node는 현재 노드의 위치, start는 구간 합의 시작, end는 구간 합의 끝을 의미합니다.

예를 들면, 1번 노드는 구간 1~8의 합으로 이루어져있으니 node=1, start=1, end=8입니다.

 

코드를 살펴보면 start==end는 leaf 노드 즉, 위 예시에서 {1, 2, 3, 4, 5, 6, 7, 8} 이것을 의미합니다. 그러므로 현재 위치에 배열의 값을 넣어줍니다. start와 end 값이 동일하므로 tree[node] = arr[end]로 작성해도 무방합니다.

 

 

leaf노드가 아닌 경우는 왼쪽과 오른쪽 노드의 합으로 이루어져있습니다. 

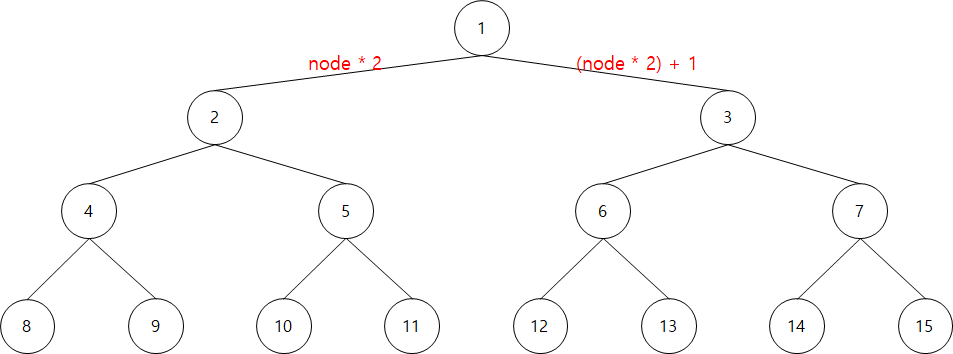
위 그림은 몇번째 노드인지 적은 내용입니다. 왼쪽 노드는 (현재 노드값*2)이고 오른쪽 노드는 (현재 노드값*2)+1임을 알 수 있습니다. 역으로 현재에서 부모 노드로 올라가려면 (현재 노드값/2)를 해주면 됩니다. 몫의 연산이므로 나머지 값은 자동으로 없어지니 홀수 노드번호에 -1과 같은 연산을 해주지 않아도 됩니다.

아무튼 이것을 적용하면 return tree[node] = init(start, mid, node*2) + init(mid+1, end, node*2+1) 이 공식이 왜 도출되었는지 이해하실 수 있을 겁니다.

 

 

 

세그먼트 트리 수정(Update)

다음으로는 값이 수정되는 경우를 알아보겠습니다.

배열의 몇번째 인덱스을 어떤 값으로 변경할 것인지 주어지면 우리는 상단부터 이 배열의 인덱스가 포함된 값들을 갱신하며 최종적으로 leaf 노드의 값까지 변경해줘야 합니다. 위에 사용한 그래프를 예시로 하여 arr[3]을 5로 변경하라는 지시 사항이 있으면 arr[3]이 포함된 모든 구간의 값을 아래 그림과 같이 변경해줘야 합니다.

 

 

이걸 코드로 변경해보면 아래와 같습니다.

void update(int start, int end, int node, int idx, long change) {
    if (idx < start || idx > end) return;   
    tree[node] += change;                   
    if (start == end) return;               
    int mid = (start + end) / 2;
    update(start, mid, node * 2, idx, change);          
    update(mid + 1, end, node * 2 + 1, idx, change);   
}

start, end는 현재 node의 구간입니다. 내가 변경해야하는 배열의 index값이 이 구간에서 벗어난다면 멈춥니다.

구간에 존재하면 그 구간 값을 변경해주고 다시 하위 노드로 탐색을 합니다. 그러다가 마지막 leaf 노드까지 변경했다면 끝나게 됩니다.

 

 

 

 

세그먼트 트리 검색(search)

마지막으로 이렇게 작성한 세그먼트 트리에서 원하는 구간의 합을 찾는 방법을 알아보겠습니다. 

구간 2~5 사이의 합을 구하는 문제가 주어지면 세그먼트 트리의 상단부터 탐색을 시작합니다. 원하는 구간보다 큰 경우 자식 노드를 탐색합니다. 그러다가 현재 노드의 범위가 원하는 구간 범위에 포함되면 그 값을 더해주며 나머지 범위에 맞는 값을 탐색합니다.

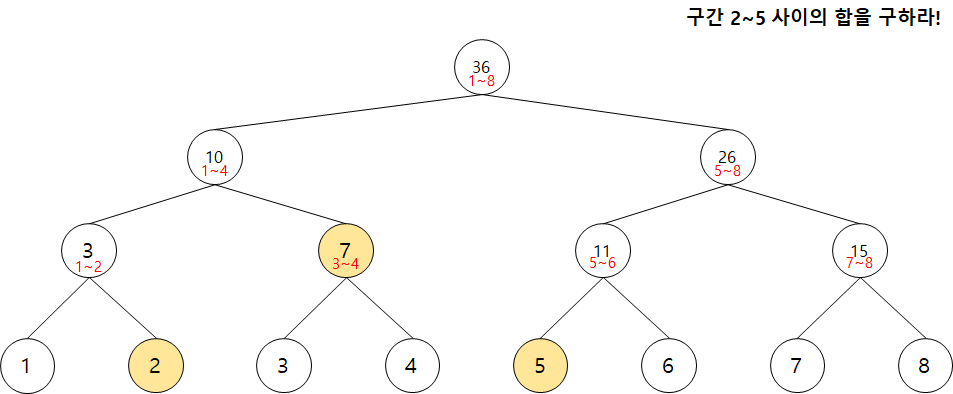
코드로 작성하면 아래와 같습니다.

long search(int start, int end, int from, int to, int node) {
    if (end < from || start > to) return 0;                         
    if (from <= start && to >= end) return tree[node];              
    int mid = (start + end) / 2;                                    
    return search(start, mid, from, to, node * 2) + search(mid + 1, end, from, to, node * 2 + 1);
}

 

 

이렇게하면 세그먼트 트리는 완성 😎